| Main index | About J. D. A. Wiseman |
Julian D. A. Wiseman
Contents: Introduction, Outline, Algorithm, Results, Strategy, Next Steps, Unimportance, Afterword.
Publication history: only here. Usual disclaimer and copyright terms apply.
The problem, as described in Mathematical Constants, Steven R. Finch, Cambridge University Press, 362-363:
We observe a fair coin being tossed repeatedly and can stop observing at any time. When we stop, the payoff is the average number of heads observed. What is the best strategy to maximize the expected payoff? Chow & Robbins [21…] described a strategy that achieves an expected payoff > 0.79 = (0.59 + 1) /2.
[21] Y.S. Chow and H. Robbins, On optimal stopping rules for sn/n, Illinois J. Math. 9 (1965) 444-454; MR 31 #4134.
Here is described an algorithm which provides strong evidence that the expected value ≈ 0.79295350640….
Let the number of heads seen so far be h, and the number of tails t, so stopping at this time would have payoff h/(h+t). Consider a restricted strategy, in which one may choose to stop or continue whilst t<4; but once t reaches 4 one must either stop or toss forever (well, until h=t which happens eventually with probability 1).
The payoff from this restricted strategy can be calculated using the following ‘spreadsheet’:
| t=0 | t=1 | t=2 | t=3 | t=4 | |
| h=0 | =Avg(↓,→) | =Avg(↓,→) | =Avg(↓,→) | =Avg(↓,→) | =Max( h/(h+t), 0.5 ) |
| h=1 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=2 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=3 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=4 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=5 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=6 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=7 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=8 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=9 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=10 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=11 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=12 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=13 | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), Avg(↓,→) ) | =Max( h/(h+t), 0.5 ) |
| h=14 | =Max( h/(h+t), 0.5 ) | =Max( h/(h+t), 0.5 ) | =Max( h/(h+t), 0.5 ) | =Max( h/(h+t), 0.5 ) | =Max( h/(h+t), 0.5 ) |
which evaluates to:
| t=0 | t=1 | t=2 | t=3 | t=4 | |
| h=0 | 599/768 | 215/384 | 349/672 | 113/224 | 1/2 |
| h=1 | 1 | 269/448 | 359/672 | 57/112 | 1/2 |
| h=2 | 1 | 2/3 | 47/84 | 29/56 | 1/2 |
| h=3 | 1 | 3/4 | 101/168 | 15/28 | 1/2 |
| h=4 | 1 | 4/5 | 2/3 | 4/7 | 1/2 |
| h=5 | 1 | 5/6 | 5/7 | 5/8 | 5/9 |
| h=6 | 1 | 6/7 | 3/4 | 2/3 | 3/5 |
| h=7 | 1 | 7/8 | 7/9 | 7/10 | 7/11 |
| h=8 | 1 | 8/9 | 4/5 | 8/11 | 2/3 |
| h=9 | 1 | 9/10 | 9/11 | 3/4 | 9/13 |
| h=10 | 1 | 10/11 | 5/6 | 10/13 | 5/7 |
| h=11 | 1 | 11/12 | 11/13 | 11/14 | 11/15 |
| h=12 | 1 | 12/13 | 6/7 | 4/5 | 3/4 |
| h=13 | 1 | 13/14 | 13/15 | 13/16 | 13/17 |
| h=14 | 1 | 14/15 | 7/8 | 14/17 | 7/9 |
where bolded numbers are stopping states in this restricted game. Already we know that the expected value of sn/n ≥ 599/768 ≈ 0.7799479166666.
Observe that the rows with h>4 are redundant: every element in the h=4 row is a stopping state, and the ‘spreadsheet’ below this can be truncated without changing the value at h=t=0.
Let EVn(h,t) be the expected value of this mini game with t ≤ n, assuming that h heads and t tails have already been tossed. We now describe the algorithm by which EVn(0,0) is calculated for large n, and when this is done we shall happily see that it appears to have a neat functional form, allowing ready approximation of the value of EV∞(0,0).
The algorithm can now proceed as follows.
| 1 | Let max_h be n. | |
| 2 | Create a one-dimensional array of maximum-precision real numbers EV[], the array being of length n+1. | |
| 3 | Fill the array with values 0.5. | EV[] is now the rightmost column in which t=n. |
| 4 | Loop from t=n−1 to 0. | |
| 5 | Set h = max_h, and EV[h] = h/(h+t). | The last row, in which h=max_h. |
| 6 | Loop over h downwards to 1. | …so going up the rows from large h to small h. |
| 7 | Calculate ( EV[h] + EV[h+1] ) / 2. | EV[h] contains the expected value of the game at h,t+1. Hence the value from tossing again is ( EV[h] + EV[h+1] ) / 2. |
| 8 | Set EV[h] to the greater of this and h/(h+t). | |
| 9 | Next h. | |
| 10 | EV[0] = ( EV[0] + EV[1] ) / 2. | This avoids the possible divide-by-zero when h=0. |
| 11 | Next t. | |
| 12 | Output EV[0]. |
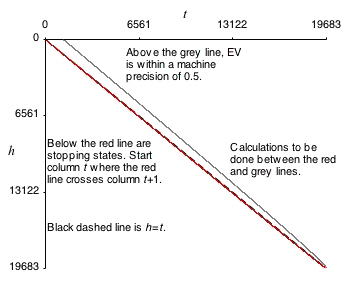
This replicates the ‘spreadsheet’ in memory linear in n. There are some improvements to this, which between them reduce the n² run-time by a factor of something like √n. The areas of calculation eliminated by these improvements are shown in the diagram on the right for n=19683; proportionately larger areas are eliminated for larger n.
A recent version of the code that implements this algorithm with improvements is available at www.jdawiseman.com/papers/easymath/coin-stopping.c. those desiring the latest version should contact the author.
It is possible to rewrite the program such that the memory usage is linear in the widest gap between the red and grey lines (rather than being linear in n), albeit at the price of a loss of readability. This recoding has not yet been attempted.
The following table shows results for n = 2i (calculations run on an Intel Pentium IV processor under Windows XP using cygwin gcc C compiler):
| i | n = 2^i | EV | Difference | Ratio | Estimated limit = EV + Diff / (1/Ratio − 1) |
|---|---|---|---|---|---|
| 1 | 2 | 0.770833333333333 | |||
| 2 | 4 | 0.779947916666666 | 0.009114583333 | ||
| 3 | 8 | 0.785247657412574 | 0.005299740746 | 0.58145727 | 0.79261028151309 |
| 4 | 16 | 0.788190898971545 | 0.002943241559 | 0.55535576 | 0.79186697529802 |
| 5 | 32 | 0.790023224424476 | 0.001832325453 | 0.62255354 | 0.79304542974422 |
| 6 | 64 | 0.791196842160634 | 0.001173617736 | 0.64050725 | 0.79328787366908 |
| 7 | 128 | 0.791897537079360 | 0.000700694919 | 0.59703845 | 0.79293570515041 |
| 8 | 256 | 0.792318224291505 | 0.000420687212 | 0.60038570 | 0.79295027021847 |
| 9 | 512 | 0.792570438324007 | 0.000252214033 | 0.59952864 | 0.79294801722604 |
| 10 | 1,024 | 0.792722493847599 | 0.000152055524 | 0.60288289 | 0.79295333676356 |
| 11 | 2,048 | 0.792814414356913 | 0.000091920509 | 0.60451937 | 0.79295492118365 |
| 12 | 4,096 | 0.792869752675300 | 0.000055338318 | 0.60202363 | 0.79295346361236 |
| 13 | 8,192 | 0.792903056616781 | 0.000033303941 | 0.60182424 | 0.79295339398384 |
| 14 | 16,384 | 0.792923109615955 | 0.000020052999 | 0.60212090 | 0.79295345634652 |
| 15 | 32,768 | 0.792935195956992 | 0.000012086341 | 0.60271987 | 0.79295353233307 |
| 16 | 65,536 | 0.792942476379465 | 0.000007280422 | 0.60236778 | 0.79295350539518 |
| 17 | 131,072 | 0.792946862428220 | 0.000004386049 | 0.60244426 | 0.79295350891743 |
| 18 | 262,144 | 0.792949504079600 | 0.000002641651 | 0.60228500 | 0.79295350449952 |
| 19 | 524,288 | 0.792951095314407 | 0.000001591235 | 0.60236367 | 0.79295350581352 |
| 20 | 1,048,576 | 0.792952053932079 | 0.000000958618 | 0.60243634 | 0.79295350654503 |
| 21 | 2,097,152 | 0.792952631391198 | 0.000000577459 | 0.60238731 | 0.79295350624769 |
| 22 | 4,194,304 | 0.792952979294206 | 0.000000347903 | 0.60247210 | 0.79295350655746 |
| 23 | 8,388,608 | 0.792953188872027 | 0.000000209578 | 0.60240302 | 0.79295350640540 |
| 24 | 16,777,216 | 0.792953315120851 | 0.000000126249 | 0.60239592 | 0.79295350639599 |
| 25 | 33,554,432 | 0.792953391174430 | 0.000000076054 | 0.60241019 | 0.79295350640739 |
| 26 | 67,108,864 | 0.792953436989929 | 0.000000045815 | 0.60241083 | 0.79295350640770 |
The same table is next shown for powers of 3:
| i | n = 3^i | EV | Difference | Ratio | Estimated limit = EV + Diff / (1/Ratio − 1) |
|---|---|---|---|---|---|
| 1 | 3 | 0.777083333333333 | |||
| 2 | 9 | 0.785866262932785 | 0.008782929599 | ||
| 3 | 27 | 0.789626479634224 | 0.003760216701 | 0.42812784 | 0.79244153793616 |
| 4 | 81 | 0.791476153990993 | 0.001849674357 | 0.49190632 | 0.79326689955370 |
| 5 | 243 | 0.792293464103993 | 0.000817310113 | 0.44186703 | 0.79294051849865 |
| 6 | 729 | 0.792657276357000 | 0.000363812253 | 0.44513367 | 0.79294913959852 |
| 7 | 2,187 | 0.792820943435251 | 0.000163667078 | 0.44986687 | 0.79295478084870 |
| 8 | 6,561 | 0.792894165592400 | 0.000073222157 | 0.44738476 | 0.79295344459041 |
| 9 | 19,683 | 0.792926925277956 | 0.000032759686 | 0.44740126 | 0.79295344854644 |
| 10 | 59,049 | 0.792941602603975 | 0.000014677326 | 0.44803013 | 0.79295351608787 |
| 11 | 177,147 | 0.792948175932809 | 0.000006573329 | 0.44785602 | 0.79295350770317 |
| 12 | 531,441 | 0.792951119086408 | 0.000002943154 | 0.44774173 | 0.79295350523929 |
| 13 | 1,594,323 | 0.792952437204528 | 0.000001318118 | 0.44785910 | 0.79295350637219 |
| 14 | 4,782,969 | 0.792953027559343 | 0.000000590355 | 0.44787702 | 0.79295350644967 |
| 15 | 14,348,907 | 0.792953291954919 | 0.000000264396 | 0.44785876 | 0.79295350641431 |
| 16 | 43,046,721 | 0.792953410364442 | 0.000000118410 | 0.44784986 | 0.79295350640660 |
Other geometrically increasing sequences of n behave likewise, including 2×3i−1; 3×2i−1; 5×2i−1; 7×2i−1; 9×2i−1; 11×2i−1; 13×2i−1; 15×2i−1; 17×2i−1; 19×2i−1; 21×2i−1; 23×2i−1; and 25×2i−1. For each of these, only the last four rows are shown here:
| i | n | EV | Difference | Ratio | Estimated limit = EV + Diff / (1/Ratio − 1) |
|---|---|---|---|---|---|
n = 2×3i−1 | |||||
| 13 | 1,062,882 | 0.792952068251885 | 0.000001772987 | 0.44783045 | 0.79295350621149 |
| 14 | 3,188,646 | 0.792952862302889 | 0.000000794051 | 0.44786062 | 0.79295350638697 |
| 15 | 9,565,938 | 0.792953217946628 | 0.000000355644 | 0.44788526 | 0.79295350645113 |
| 16 | 28,697,814 | 0.792953377218624 | 0.000000159272 | 0.44784142 | 0.79295350639998 |
n = 3×2i−1 | |||||
| 22 | 6,291,456 | 0.792953114533501 | 0.000000258644 | 0.60243695 | 0.79295350646377 |
| 23 | 12,582,912 | 0.792953270339568 | 0.000000155806 | 0.60239469 | 0.79295350639463 |
| 24 | 25,165,824 | 0.792953364197547 | 0.000000093858 | 0.60240260 | 0.79295350640243 |
| 25 | 50,331,648 | 0.792953420738771 | 0.000000056541 | 0.60241254 | 0.79295350640833 |
n = 5×2i−1 | |||||
| 22 | 10,485,760 | 0.792953236675307 | 0.000000178026 | 0.60239696 | 0.79295350639723 |
| 23 | 20,971,520 | 0.792953343917754 | 0.000000107242 | 0.60239801 | 0.79295350639842 |
| 24 | 41,943,040 | 0.792953408522001 | 0.000000064604 | 0.60241303 | 0.79295350640861 |
| 25 | 83,886,080 | 0.792953447440291 | 0.000000038918 | 0.60241071 | 0.79295350640766 |
n = 7×2i−1 | |||||
| 21 | 7,340,032 | 0.792953156304784 | 0.000000231073 | 0.60241671 | 0.79295350642634 |
| 22 | 14,680,064 | 0.792953295502404 | 0.000000139198 | 0.60239569 | 0.79295350639561 |
| 23 | 29,360,128 | 0.792953379356017 | 0.000000083854 | 0.60240694 | 0.79295350640552 |
| 24 | 58,720,256 | 0.792953429870388 | 0.000000050514 | 0.60241139 | 0.79295350640787 |
n = 9×2i−1 | |||||
| 21 | 9,437,184 | 0.792953215074249 | 0.000000192283 | 0.60239934 | 0.79295350640012 |
| 22 | 18,874,368 | 0.792953330905141 | 0.000000115831 | 0.60239692 | 0.79295350639717 |
| 23 | 37,748,736 | 0.792953400683046 | 0.000000069778 | 0.60241188 | 0.79295350640813 |
| 24 | 75,497,472 | 0.792953442718023 | 0.000000042035 | 0.60241099 | 0.79295350640774 |
n = 11×2i−1 | |||||
| 20 | 5,767,168 | 0.792953088791376 | 0.000000275635 | 0.60244710 | 0.79295350648587 |
| 21 | 11,534,336 | 0.792953254832655 | 0.000000166041 | 0.60239494 | 0.79295350639491 |
| 22 | 23,068,672 | 0.792953354855966 | 0.000000100023 | 0.60240027 | 0.79295350640051 |
| 23 | 46,137,344 | 0.792953415111305 | 0.000000060255 | 0.60241296 | 0.79295350640854 |
n = 13×2i−1 | |||||
| 20 | 6,815,744 | 0.792953136810324 | 0.000000243941 | 0.60242671 | 0.79295350644375 |
| 21 | 13,631,488 | 0.792953283759023 | 0.000000146949 | 0.60239524 | 0.79295350639518 |
| 22 | 27,262,976 | 0.792953372281616 | 0.000000088523 | 0.60240474 | 0.79295350640401 |
| 23 | 54,525,952 | 0.792953425608702 | 0.000000053327 | 0.60241216 | 0.79295350640817 |
n = 15×2i−1 | |||||
| 20 | 7,864,320 | 0.792953173528347 | 0.000000219705 | 0.60240697 | 0.79295350641128 |
| 21 | 15,728,640 | 0.792953305877818 | 0.000000132349 | 0.60239574 | 0.79295350639569 |
| 22 | 31,457,280 | 0.792953385606316 | 0.000000079728 | 0.60240889 | 0.79295350640670 |
| 23 | 62,914,560 | 0.792953433635636 | 0.000000048029 | 0.60241094 | 0.79295350640773 |
n = 17×2i−1 | |||||
| 20 | 8,912,896 | 0.792953202640363 | 0.000000200490 | 0.60240124 | 0.79295350640269 |
| 21 | 17,825,792 | 0.792953323414915 | 0.000000120775 | 0.60239637 | 0.79295350639652 |
| 22 | 35,651,584 | 0.792953396170865 | 0.000000072756 | 0.60241127 | 0.79295350640790 |
| 23 | 71,303,168 | 0.792953439999837 | 0.000000043829 | 0.60241082 | 0.79295350640770 |
n = 19×2i−1 | |||||
| 19 | 4,980,736 | 0.792953041537121 | 0.000000306823 | 0.60246218 | 0.79295350652302 |
| 20 | 9,961,472 | 0.792953226366925 | 0.000000184830 | 0.60239806 | 0.79295350639854 |
| 21 | 19,922,944 | 0.792953337707907 | 0.000000111341 | 0.60239734 | 0.79295350639770 |
| 22 | 39,845,888 | 0.792953404781104 | 0.000000067073 | 0.60241248 | 0.79295350640837 |
n = 21×2i−1 | |||||
| 19 | 5,505,024 | 0.792953074341674 | 0.000000285172 | 0.60245230 | 0.79295350649762 |
| 20 | 11,010,048 | 0.792953246128268 | 0.000000171787 | 0.60239617 | 0.79295350639635 |
| 21 | 22,020,096 | 0.792953349612308 | 0.000000103484 | 0.60239881 | 0.79295350639922 |
| 22 | 44,040,192 | 0.792953411952475 | 0.000000062340 | 0.60241334 | 0.79295350640873 |
n = 23×2i−1 | |||||
| 19 | 6,029,312 | 0.792953102146911 | 0.000000266820 | 0.60244184 | 0.79295350647418 |
| 20 | 12,058,624 | 0.792953262877942 | 0.000000160731 | 0.60239471 | 0.79295350639462 |
| 21 | 24,117,248 | 0.792953359702563 | 0.000000096825 | 0.60240155 | 0.79295350640158 |
| 22 | 48,234,496 | 0.792953418030943 | 0.000000058328 | 0.60241269 | 0.79295350640840 |
n = 25×2i−1 | |||||
| 19 | 6,553,600 | 0.792953126057606 | 0.000000251038 | 0.60243188 | 0.79295350645355 |
| 20 | 13,107,200 | 0.792953277281640 | 0.000000151224 | 0.60239496 | 0.79295350639492 |
| 21 | 26,214,400 | 0.792953368379547 | 0.000000091098 | 0.60240363 | 0.79295350640322 |
| 22 | 52,428,800 | 0.792953423258054 | 0.000000054879 | 0.60241238 | 0.79295350640826 |
This lacks a proof that the ratio tends to a constant limit. But even if the ratio merely changes slowly, then the estimated limit should still be good. Hence the claim that this algorithm “provides strong evidence that the expected value ≈ 0.79295350640…”, with the next digit probably being not more than 1 different from 7.
This also lacks a proof that the limit of the restricted strategy is indeed the value of the whole game. But small changes to the algorithm (present but deactivated in the code) allow calculation of the probability of reaching the rightmost boundary at t=max_t, and this probability appears to be proportional to n−0.231…. As n tends to +∞ this probability tends to 0, suggesting that the boundary becomes irrelevant in the limit. Which is encouraging.
For these sequences the raw output data is available:
| Scores | n = 3i; 2×3i−1; 2i; 3×2i−1; 5×2i−1; 7×2i−1; 9×2i−1; 11×2i−1; 13×2i−1; 17×2i−1; 19×2i−1; 21×2i−1; 23×2i−1; 25×2i−1 |
| Strategy | t≤2048, n = 3i; 2×3i−1; 2i; 3×2i−1; 5×2i−1; 7×2i−1; 9×2i−1; 11×2i−1; 13×2i−1; 17×2i−1; 19×2i−1; 21×2i−1; 23×2i−1; 25×2i−1 |
| Precision | Some t, n = 3i; 2×3i−1; 2i; 3×2i−1; 5×2i−1; 7×2i−1; 9×2i−1; 11×2i−1; 13×2i−1; 17×2i−1; 19×2i−1; 21×2i−1; 23×2i−1; 25×2i−1 |
| Scores n = 226; Strategy t≤26(216−2), t≡0 mod 64, n = 226; Precision Some t, n = 226 | |
![(h[t]−t)/√t as a function of t](coin-root-t.gif)
![(h[t]−t)/√(h[t]+t) as a function of t](coin-root-tosses.gif)
The above process estimates the value of the game as a limit, without specifying the strategy that would achieve that limit. Specifying the strategy is not easy: if n=1,048,576 then h=177 and t=162 is a stopping point. But with n twice as big it becomes profitable to keep playing: with 162 tails one would need at least 178 heads to stop. Let h[t] be, for any value of t, the largest number of heads with which one would toss again. The algorithm does not provide a direct estimate of h[t], but we can guess that with t<<n, the algorithm’s estimate is close.
The upper chart on the right, with the dark blue line, shows ( h[t] − t ) / √t. This is not quite a horizontal line, though over a huge t range does not vary much. We might guess that ( h[t] − t ) is, in the limit, ≤O(√t). The lower chart, with the dark green line, replaces “√t” with “√( h[t] + t )”, and this make no difference to the conclusion: stopping states require that the number of heads exceed the number of tails by something of the order of something no greater than the square root of the number of tails, or the square root of the number of tosses. The author has failed to find a better-behaving more-plausible combination of √t, Ln(t), and Ln(Ln(t)).
For large increases in CPU time (and perhaps memory), this algorithm could calculate a few more decimal places of accuracy. Readers with CPU time and memory to spare are invited to cope.
But an algorithmic improvement is needed to calculate many more decimal places, which might work by better estimating the value of the game on the boundary, and then using backward induction from this improved estimate. The above algorithm estimates the boundary values as Max( h/(h+t), ½). A better estimate might come from solving a continuous version of the game, and using that value on the boundary. A solution to such a continuous version might perhaps have the following properties.
∃ function EV[h,t], with ½≤EV[h,t]≤1 ∀h≥0, t≥0, h t>0, representing the value of the continuous game (the rules of which have not been specified) after h heads and t tails.
∃ continuous stopping function h[t]≥t, monotonically increasing in t ∀t>0, such that h≥h[t] ⇒ EV[h,t]=h/(h+t).
∀ t and h such that 0<t and 0<h<h[t], EV[h,t] is continuous and once partially differentiable in h and t. EV[h,t] is also continuous on the h=h[t] boundary.
h<h[t] ⇒ ∂EV[h,t]/∂h = −∂EV[h,t]/∂t. This is the analogue of the “Avg(↓,→)” from the discrete game.
∀ fixed h, as t tends to +∞ the limit of EV[h,t] is ½. This defines the rightmost ‘boundary’.
Then h[t] is chosen to maximise EV[0,t′], for some t′>0. (It is suspected that replacing t′ with a smaller positive value would leave h[t] unchanged for t>t′. Hopefully this would be clear from the functional form of ht′[t].)
A solution would be an estimate of the value of the discrete game for large h and t. An analytical solution could be used to generate the starting values of the backward induction, substantially improving the estimate of sn/n. Mathematicians skilled in partial differential equations are invited to help. All, whether or not skilled mathematicians, are invited to invite skilled mathematicians to www.jdawiseman.com/papers/easymath/coin-stopping.html. Please, somebody help. (This request for help is echoed in Open Mathematical Questions at jdawiseman.com.)
Pretend for a moment that this puzzle has an expected value that is some combination of elementary mathematical constants and functions. If this were true, the game would, in some way, illuminate a property of those constants and functions. There would be a connection between this puzzle and the rest of mathematics.
But the Inverse Symbolic Calculator at the Centre for Experimental and Constructive Mathematics does not know of any such combination for even the first eight digits of the limit (“0.79295350”). So it seems likely that this problem is of no importance whatsoever, even if it has given the author a little entertainment.
Julian D. A. Wiseman
October and November 2005
In June 2009 this paper was cited: Luis A. Medina & Doron Zeilberger, ‘An Experimental Mathematics Perspective on the Old, and still Open, Question of When To Stop?’, arXiv:0907.0032.
September 2010: Medina and Zeilberger asked whether one should stop at h=5 t=3. This is answered in the affirmative by The Chow & Robbins Problem: Stop at h=5 t=3.
January 2012: this paper was cited by Olle Häggström and Johan Wästlund in ‘Rigorous computer analysis of the Chow-Robbins game’, arXiv:1201.0626.
In March 2012 this paper was cited in Stochastic Games and Dynamic Programming, by Professor Henk Tijms, published in the July 2012 issue of the Asia Pacific Math Newsletter.
August 2012: in the above analysis, estimates of the limiting value were obtained from by considering three values of the restricted game, always from n’s in geometric progression. But it cannot be optimal to take just three data points at a time. Surely one could derive a better estimate by considering all the data simultaneously. Presumably the fitting must be done with a greater weight given to larger n’s, and hopefully in a manner that still allowed an estimate of the uncertainty about the limiting value. Help from a competent statistician would be greatly welcomed.
March 2013: help was sought on MathOverflow.net: The Chow & Robbins game ≈ 0.79295350640: improvements could come from simple statistics, or from a continuous version of the game. And help came: hurray!
September 2013: the problem had previously been discussed with friend Phil Wakely, who has extended the calculation and its precision. His paper agrees with “0.7929535064”, but not necessarily the next 0, and hence has even less support for “the next digit probably being not more than 1 different from 7”. So this author’s last 1½ decimal places should be considered speculative rather than known.
The results suggest EV(0,0)=0.7929535064… Note that this is one less digit of precision than in the conjecture from [1] ("the expected value ≈0.79295350640…, with the next digit probably being not more than 1 different from 7") as despite the increased precision and larger n computation, the ratio of deltas between successive EV(0,0) estimates with increasing n does not as yet seem to be converging sufficiently.
(Also note that our definitions of n differ by a factor of 2, as is apparent from the tables of results.)
| Main index | Top | About J. D. A. Wiseman |