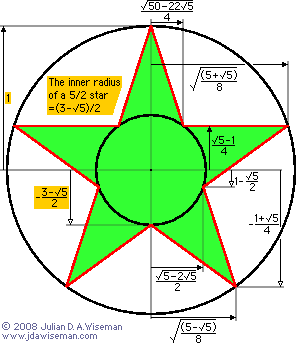
The inner radius of a 5/2 star is (3–√5)/2

The horizontal line that divides the 5/2 star into two equal areas is at y = ¼(5√5–11) ≈ 0.04508497, which touches the star at x = ±½√(½(5–√5)) ≈ ±0.587785.

Excel formulae for plotting a unit 5/2 star;
range names having a two-pixel black border.

Sqrt5	Star_5_2_Area
= Sqrt(5)	= Sqrt(50 - 22Sqrt5) 5/4

Star_5_2_X	Star_5_2_Y
= 0	= 1
= Sqrt(50 - 22*Sqrt5) / 4	= (Sqrt5 - 1) / 4
= Sqrt( (5+Sqrt5) / 8 )	= (Sqrt5 - 1) / 4
= Sqrt(5 - 2*Sqrt5) / 2	= 1 - Sqrt5/2
= Sqrt( (5-Sqrt5) / 8 )	= -(1 + Sqrt5) / 4
= 0	= (Sqrt5 - 3) / 2
= -Sqrt( (5-Sqrt5) / 8 )	= -(1 + Sqrt5) / 4
= -Sqrt(5 - 2*Sqrt5) / 2	= 1 - Sqrt5/2
= -Sqrt( (5+Sqrt5) / 8 )	= (Sqrt5 - 1) / 4
= -Sqrt(50 - 22*Sqrt5) / 4	= (Sqrt5 - 1) / 4
= 0	= 1

The Inner Radius of n/m Stars, in Surds

Julian D. A. Wiseman

Contents: if the boundary of an n/m star is drawn, there are n points on the exterior bounding circle, and another n points on an interior circle (see diagram). The table below shows, in surds, the radius of this interior circle, for several values of n and m: n/m general case, 5/2, 6/2, 8/2, 8/3, 10/2, 10/3, 10/4, 12/2, 12/3, 12/4, 12/5, 15/2, 15/3, 15/4, 15/5, 15/6, 15/7, 16/2, 16/3, 16/4, 16/5, 16/6, 16/7, 20/2, 20/3, 20/4, 20/5, 20/6, 20/7, 20/8, and 20/9.

Publication history: only here. Usual disclaimer and copyright terms apply. Also see the values of Sin[] and Cos[] in surds, the values of Cosecant[] = Cosec[] = Csc[] = 1/Sin[] and Secant[] = Sec[] = 1/Cos[] in surds, and the values of Tan[] in surds.

If the boundary of an n/m star is drawn, there are n points on the exterior bounding circle, and another n points on an interior circle (see diagram on right). The table below shows, in surds, the radius of this interior circle, for several values of n and m. The surds are are shown in several formats.

Graphical formula: a .png, derived from…
LaTex: a LaTeX expression.
Excel: copy-pasteable into Excel, which will automatically convert the “Sqrt” into an upper-case “SQRT”.
CalcCenter: if one enters Sqrt[2] directly into Mathematica CalcCenter (the budget version of Mathematica), it automatically evaluates the expression numerically, frustrating an attempt to work with surds. To prevent this integers inside the inner-most Sqrts have been replaced with the likes of Int5, which CalcCenter treats as a variable. If using the full-expense Mathematica instances of “Int” may be removed by a preprocessor or by setting Int2=2; Int3=3; Int5=5;.
Postscript: using 3 5 sqrt sub 2 div rather than 180 5 div dup 2 mul cos exch cos div is about as efficient computationally, but is, in some sense, far more elegant.

Help! Endeavours have been made to represent these values as simply as possible. But further simplifications would be welcomed, credit being given.

Trivia: as m→+∞ with k fixed, the inner radius of the (2m+k)/m star tends downwards to k/(2+k) + m^–2×π²k(k+1)/(24(k+2)) + O(m^–4), and hence the inner radii are bounded below by ⅓.

Open question: stars (6i–2)/i and (18i–6)/(6i–2) have the same inner radius, as do (6i–4)/i and (18i–12)/(6i–3), for integer i≥2 (PDF of overlapping 8/2 and 24/9 stars, and of 10/2 and 30/10 and 14/3 and 42/15 stars), as is easily shown using the product-to-sum formulae. But are all pairs of stars with matching inner radii in one of these two forms?—a question discussed in greater detail in Open Mathematical Questions at jdawiseman.com. A proof (or, less probably, a counterexample) would be welcomed. Also observe that the inner radius of both forms tends to unity, being >0.99 when i≥31, and >0.99975 when i≥1210.

Errors: whilst the outputs have been tested, it is possible that errors remain. Please do test things before embedding them somewhere important—and if errors or possible improvements are found, tell the author.

n/m	Approximate inner radius	LaTeX	Excel	CalcCenter	PostScript
n/m		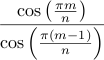\frac{\cos{\left(\frac{\pi m}{n}\right)}}{\cos{\left(\frac{\pi (m-1)}{n}\right)}}	=Cos(Pi()m/n) / Cos(Pi()(m-1)/n)	Cos[π m / n] / Cos[π (m-1) / n]	`m n 180 exch div 2 copy mul cos 3 1 roll exch 1 sub mul cos div`
5/2	≈ 0.38196601125	\frac{1}{2} \left(3 - \sqrt{5}\right)	=(3-Sqrt(5))/2	(3-Sqrt[Int5])/2	`3 5 sqrt sub 2 div`
6/2	≈ 0.57735026919	\frac{\sqrt{3}}{3}	=Sqrt(3)/3	Sqrt[Int3]/3	`3 sqrt 3 div`
8/2	≈ 0.76536686473	\sqrt{2 - \sqrt{2}}	=Sqrt(2-Sqrt(2))	Sqrt[2-Sqrt[Int2]]	`2 2 sqrt sub sqrt`
8/3	≈ 0.541196100146	\frac{1}{2} \sqrt{4 - 2 \sqrt{2}}	=Sqrt(4-2*Sqrt(2))/2	Sqrt[4-2 Sqrt[Int2]]/2	`4 2 sqrt 2 mul sub sqrt 2 div`
10/2	≈ 0.850650808352	\sqrt{\frac{1}{10} \left(5 + \sqrt{5}\right)}	=Sqrt( (5+Sqrt(5)) / 10 )	Sqrt[ (5+Sqrt[Int5]) / 10 ]	`5 5 sqrt add 10 div sqrt`
10/3	≈ 0.726542528005	\sqrt{5 - 2 \sqrt{5}}	=Sqrt(5-2*Sqrt(5))	Sqrt[5-2 Sqrt[Int5]]	`5 5 sqrt 2 mul sub sqrt`
10/4	≈ 0.525731112119	\frac{1}{10} \sqrt{50 - 10 \sqrt{5}}	=Sqrt(50-10*Sqrt(5))/10	Sqrt[50-10 Sqrt[Int5]]/10	`50 5 sqrt 10 mul sub sqrt 10 div`
12/2	≈ 0.896575472168	\frac{\sqrt{2} }{2}\left(3 - \sqrt{3}\right)	=Sqrt(2) * (3-Sqrt(3)) / 2	Sqrt[Int2] (3-Sqrt[Int3]) / 2	`3 3 sqrt sub 2 sqrt mul 2 div`
12/3	≈ 0.816496580928	\frac{\sqrt{6}}{3}	=Sqrt(6)/3	Sqrt[Int2 Int3]/3	`6 sqrt 3 div`
12/4	≈ 0.707106781187	\frac{\sqrt{2}}{2}	=Sqrt(2)/2	Sqrt[Int2]/2	`2 sqrt 2 div`
12/5	≈ 0.517638090205	\frac{\sqrt{2} }{2}\left(\sqrt{3} - 1\right)	=Sqrt(2) * (Sqrt(3)-1) / 2	Sqrt[Int2] (Sqrt[Int3]-1) / 2	`3 sqrt 1 sub 2 sqrt mul 2 div`
15/2	≈ 0.933954606603	\frac{1}{4} \left(5 \sqrt{5} + \sqrt{150 - 66 \sqrt{5}} - 9\right)	=( 5Sqrt(5) + Sqrt(150-66Sqrt(5)) - 9 ) / 4	( 5 Sqrt[Int5] + Sqrt[150-66 Sqrt[Int5]] - 9 ) / 4	`5 sqrt dup -66 mul 150 add sqrt exch 5 mul add 9 sub 4 div`
15/3	≈ 0.885579351971	\frac{1}{4} \left(\sqrt{150 + 66 \sqrt{5}} - 3 \sqrt{5} - 7\right)	=( Sqrt(150+66Sqrt(5)) - 3Sqrt(5) - 7 ) / 4	( Sqrt[150+66 Sqrt[Int5]] - 3 Sqrt[Int5] - 7 ) / 4	`5 sqrt dup 66 mul 150 add sqrt exch 3 mul sub 7 sub 4 div`
15/4	≈ 0.827090915285	\frac{1}{4} \left(\sqrt{30 - 6 \sqrt{5}} + \sqrt{5} - 3\right)	=( Sqrt(30-6*Sqrt(5)) + Sqrt(5) - 3 ) / 4	( Sqrt[30-6 Sqrt[Int5]] + Sqrt[Int5] - 3 ) / 4	`5 sqrt dup -6 mul 30 add sqrt add 3 sub 4 div`
15/5	≈ 0.747238274932	\frac{1}{2} \left(\sqrt{15 - 6 \sqrt{5}} + \sqrt{5} - 2\right)	=( Sqrt(15-6*Sqrt(5)) + Sqrt(5) - 2 ) / 2	( Sqrt[15-6 Sqrt[Int5]] + Sqrt[Int5] - 2 ) / 2	`5 sqrt dup -6 mul 15 add sqrt add 2 sub 2 div`
15/6	≈ 0.61803398875	\frac{1}{2} \left(\sqrt{5} - 1\right)	=(Sqrt(5)-1)/2	(Sqrt[Int5]-1)/2	`5 sqrt 1 sub 2 div`
15/7	≈ 0.338261212718	\frac{1}{4} \left(\sqrt{30 + 6 \sqrt{5}} - \sqrt{5} - 3\right)	=( Sqrt(30+6*Sqrt(5)) - Sqrt(5) - 3 ) / 4	( Sqrt[30+6 Sqrt[Int5]] - Sqrt[Int5] - 3 ) / 4	`5 sqrt dup 6 mul 30 add sqrt sub neg 3 sub 4 div`
16/2	≈ 0.941979402598	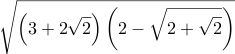\sqrt{\left(3 + 2 \sqrt{2}\right) \left(2 - \sqrt{2 + \sqrt{2}}\right)}	=Sqrt( (3+2Sqrt(2)) (2-Sqrt(2+Sqrt(2))) )	Sqrt[ (3+2 Sqrt[Int2]) (2-Sqrt[2+Sqrt[Int2]]) ]	`2 sqrt dup 2 mul 3 add exch 2 add sqrt 2 sub neg mul sqrt`
16/3	≈ 0.899976223136	\sqrt{\frac{1}{2} \sqrt{20 - 14 \sqrt{2}} - \sqrt{2} + 2}	=Sqrt( Sqrt(20-14*Sqrt(2))/2 - Sqrt(2) + 2 )	Sqrt[ Sqrt[20-14 Sqrt[Int2]]/2 - Sqrt[Int2] + 2 ]	`2 sqrt neg dup 14 mul 20 add sqrt 2 div add 2 add sqrt`
16/4	≈ 0.850430094767	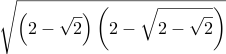\sqrt{\left(2 - \sqrt{2}\right) \left(2 - \sqrt{2 - \sqrt{2}}\right)}	=Sqrt( (2-Sqrt(2)) * (2-Sqrt(2-Sqrt(2))) )	Sqrt[ (2-Sqrt[Int2]) (2-Sqrt[2-Sqrt[Int2]]) ]	`2 2 sqrt sub dup sqrt 2 sub neg mul sqrt`
16/5	≈ 0.785694958387	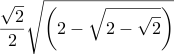\frac{\sqrt{2} }{2}\sqrt{\left(2 - \sqrt{2 - \sqrt{2}}\right)}	=Sqrt(2) * Sqrt( (2-Sqrt(2-Sqrt(2))) ) / 2	Sqrt[Int2] Sqrt[ (2-Sqrt[2-Sqrt[Int2]]) ] / 2	`2 sqrt dup 2 sub neg sqrt 2 sub neg sqrt mul 2 div`
16/6	≈ 0.688811980234	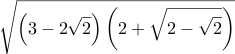\sqrt{\left(3 - 2 \sqrt{2}\right) \left(2 + \sqrt{2 - \sqrt{2}}\right)}	=Sqrt( (3-2Sqrt(2)) (2+Sqrt(2-Sqrt(2))) )	Sqrt[ (3-2 Sqrt[Int2]) (2+Sqrt[2-Sqrt[Int2]]) ]	`2 sqrt neg dup 2 add sqrt 2 add exch 2 mul 3 add mul sqrt`
16/7	≈ 0.509795579104	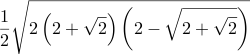\frac{1}{2} \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 - \sqrt{2 + \sqrt{2}}\right)}	=Sqrt( 2 * (2+Sqrt(2)) * (2-Sqrt(2+Sqrt(2))) ) / 2	Sqrt[ 2 (2+Sqrt[Int2]) (2-Sqrt[2+Sqrt[Int2]]) ] / 2	`2 sqrt 2 add dup sqrt 2 sub neg mul 2 mul sqrt 2 div`
20/2	≈ 0.962911555402	\frac{1}{2} \sqrt{25 + 11 \sqrt{5}} - \frac{\sqrt{2}}{4}\left(\sqrt{5} + 5\right)	=Sqrt(25+11Sqrt(5))/2 - Sqrt(2)(Sqrt(5)+5)/4	Sqrt[25+11 Sqrt[Int5]]/2 - Sqrt[Int2] (Sqrt[Int5]+5)/4	`5 sqrt dup 11 mul 25 add sqrt 2 div exch 5 add 2 sqrt mul 4 div sub`
20/3	≈ 0.936859701734	\frac{\sqrt{2} }{10}\left(\sqrt{25 - 10 \sqrt{5}} + 5\right)	=Sqrt(2) * ( Sqrt(25-10*Sqrt(5)) + 5 ) / 10	Sqrt[Int2] ( Sqrt[25-10 Sqrt[Int5]] + 5 ) / 10	`25 5 sqrt 10 mul sub sqrt 5 add 2 sqrt mul 10 div`
20/4	≈ 0.907980999479	\frac{1}{4} \left(2 \sqrt{\sqrt{5} + 5} - \sqrt{2} \left(\sqrt{5} - 1\right)\right)	=( 2Sqrt(Sqrt(5)+5) - Sqrt(2)(Sqrt(5)-1) ) / 4	( 2 Sqrt[Sqrt[Int5]+5] - Sqrt[Int2] (Sqrt[Int5]-1) ) / 4	`5 sqrt dup 5 add sqrt 2 mul exch 1 sub 2 sqrt mul sub 4 div`
20/5	≈ 0.874032048898	\frac{\sqrt{2} }{2}\left(\sqrt{5} - 1\right)	=Sqrt(2) * (Sqrt(5)-1) / 2	Sqrt[Int2] (Sqrt[Int5]-1) / 2	`5 sqrt 1 sub 2 sqrt mul 2 div`
20/6	≈ 0.831253875555	\frac{1}{2} \sqrt{5 - \sqrt{5}}	=Sqrt(5-Sqrt(5))/2	Sqrt[5-Sqrt[Int5]]/2	`5 5 sqrt sub sqrt 2 div`
20/7	≈ 0.772374771175	\frac{\sqrt{2}}{4}\left(\sqrt{5} + 1\right) - \frac{1}{10} \sqrt{25 - 5 \sqrt{5}}	=Sqrt(2)(Sqrt(5)+1)/4 - Sqrt(25-5Sqrt(5))/10	Sqrt[Int2] (Sqrt[Int5]+1)/4 - Sqrt[25-5 Sqrt[Int5]]/10	`5 sqrt dup 1 add 2 sqrt mul 4 div exch -5 mul 25 add sqrt 10 div sub`
20/8	≈ 0.680668416084	\frac{1}{2} \left(\sqrt{10 - 4 \sqrt{5}} + \sqrt{2} \left(\sqrt{5} - 2\right)\right)	=( Sqrt(10-4Sqrt(5)) + Sqrt(2)(Sqrt(5)-2) ) / 2	( Sqrt[10-4 Sqrt[Int5]] + Sqrt[Int2] (Sqrt[Int5]-2) ) / 2	`5 sqrt dup -4 mul 10 add sqrt exch 2 sub 2 sqrt mul add 2 div`
20/9	≈ 0.506232562894	\frac{\sqrt{2}}{4}\left(\sqrt{5} + 3\right) - \frac{1}{2} \sqrt{\sqrt{5} + 5}	=Sqrt(2)*(Sqrt(5)+3)/4 - Sqrt(Sqrt(5)+5)/2	Sqrt[Int2] (Sqrt[Int5]+3)/4 - Sqrt[Sqrt[Int5]+5]/2	`5 sqrt dup 3 add 2 sqrt mul 4 div exch 5 add sqrt 2 div sub`

Afterwords

October 2026, stars in the table were changed from PNG to SVG. Many such follow.

3: Polygon 3 4: Polygon 4 5: Polygon 5 Star 5⁄2 6: Polygon 6 Star 6⁄2 7: Polygon 7 Star 7⁄2 Star 7⁄3 8: Polygon 8 Star 8⁄2 Star 8⁄3 9: Polygon 9 Star 9⁄2 Star 9⁄3 Star 9⁄4 10: Polygon 10 Star 10⁄2 Star 10⁄3 Star 10⁄4 11: Polygon 11 Star 11⁄2 Star 11⁄3 Star 11⁄4 Star 11⁄5 12: Polygon 12 Star 12⁄2 Star 12⁄3 Star 12⁄4 Star 12⁄5 13: Polygon 13 Star 13⁄2 Star 13⁄3 Star 13⁄4 Star 13⁄5 Star 13⁄6 14: Polygon 14 Star 14⁄2 Star 14⁄3 Star 14⁄4 Star 14⁄5 Star 14⁄6 15: Polygon 15 Star 15⁄2 Star 15⁄3 Star 15⁄4 Star 15⁄5 Star 15⁄6 Star 15⁄7 16: Polygon 16 Star 16⁄2 Star 16⁄3 Star 16⁄4 Star 16⁄5 Star 16⁄6 Star 16⁄7 17: Polygon 17 Star 17⁄2 Star 17⁄3 Star 17⁄4 Star 17⁄5 Star 17⁄6 Star 17⁄7 Star 17⁄8 18: Polygon 18 Star 18⁄2 Star 18⁄3 Star 18⁄4 Star 18⁄5 Star 18⁄6 Star 18⁄7 Star 18⁄8 19: Polygon 19 Star 19⁄2 Star 19⁄3 Star 19⁄4 Star 19⁄5 Star 19⁄6 Star 19⁄7 Star 19⁄8 Star 19⁄9 20: Polygon 20 Star 20⁄2 Star 20⁄3 Star 20⁄4 Star 20⁄5 Star 20⁄6 Star 20⁄7 Star 20⁄8 Star 20⁄9 21: Polygon 21 Star 21⁄2 Star 21⁄3 Star 21⁄4 Star 21⁄5 Star 21⁄6 Star 21⁄7 Star 21⁄8 Star 21⁄9 Star 21⁄10 22: Polygon 22 Star 22⁄2 Star 22⁄3 Star 22⁄4 Star 22⁄5 Star 22⁄6 Star 22⁄7 Star 22⁄8 Star 22⁄9 Star 22⁄10 23: Polygon 23 Star 23⁄2 Star 23⁄3 Star 23⁄4 Star 23⁄5 Star 23⁄6 Star 23⁄7 Star 23⁄8 Star 23⁄9 Star 23⁄10 Star 23⁄11 24: Polygon 24 Star 24⁄2 Star 24⁄3 Star 24⁄4 Star 24⁄5 Star 24⁄6 Star 24⁄7 Star 24⁄8 Star 24⁄9 Star 24⁄10 Star 24⁄11 25: Polygon 25 Star 25⁄2 Star 25⁄3 Star 25⁄4 Star 25⁄5 Star 25⁄6 Star 25⁄7 Star 25⁄8 Star 25⁄9 Star 25⁄10 Star 25⁄11 Star 25⁄12 26: Polygon 26 Star 26⁄2 Star 26⁄3 Star 26⁄4 Star 26⁄5 Star 26⁄6 Star 26⁄7 Star 26⁄8 Star 26⁄9 Star 26⁄10 Star 26⁄11 Star 26⁄12 27: Polygon 27 Star 27⁄2 Star 27⁄3 Star 27⁄4 Star 27⁄5 Star 27⁄6 Star 27⁄7 Star 27⁄8 Star 27⁄9 Star 27⁄10 Star 27⁄11 Star 27⁄12 Star 27⁄13 28: Polygon 28 Star 28⁄2 Star 28⁄3 Star 28⁄4 Star 28⁄5 Star 28⁄6 Star 28⁄7 Star 28⁄8 Star 28⁄9 Star 28⁄10 Star 28⁄11 Star 28⁄12 Star 28⁄13 29: Polygon 29 Star 29⁄2 Star 29⁄3 Star 29⁄4 Star 29⁄5 Star 29⁄6 Star 29⁄7 Star 29⁄8 Star 29⁄9 Star 29⁄10 Star 29⁄11 Star 29⁄12 Star 29⁄13 Star 29⁄14 30: Polygon 30 Star 30⁄2 Star 30⁄3 Star 30⁄4 Star 30⁄5 Star 30⁄6 Star 30⁄7 Star 30⁄8 Star 30⁄9 Star 30⁄10 Star 30⁄11 Star 30⁄12 Star 30⁄13 Star 30⁄14 31: Polygon 31 Star 31⁄2 Star 31⁄3 Star 31⁄4 Star 31⁄5 Star 31⁄6 Star 31⁄7 Star 31⁄8 Star 31⁄9 Star 31⁄10 Star 31⁄11 Star 31⁄12 Star 31⁄13 Star 31⁄14 Star 31⁄15 32: Polygon 32 Star 32⁄2 Star 32⁄3 Star 32⁄4 Star 32⁄5 Star 32⁄6 Star 32⁄7 Star 32⁄8 Star 32⁄9 Star 32⁄10 Star 32⁄11 Star 32⁄12 Star 32⁄13 Star 32⁄14 Star 32⁄15 33: Polygon 33 Star 33⁄2 Star 33⁄3 Star 33⁄4 Star 33⁄5 Star 33⁄6 Star 33⁄7 Star 33⁄8 Star 33⁄9 Star 33⁄10 Star 33⁄11 Star 33⁄12 Star 33⁄13 Star 33⁄14 Star 33⁄15 Star 33⁄16 34: Polygon 34 Star 34⁄2 Star 34⁄3 Star 34⁄4 Star 34⁄5 Star 34⁄6 Star 34⁄7 Star 34⁄8 Star 34⁄9 Star 34⁄10 Star 34⁄11 Star 34⁄12 Star 34⁄13 Star 34⁄14 Star 34⁄15 Star 34⁄16 35: Polygon 35 Star 35⁄2 Star 35⁄3 Star 35⁄4 Star 35⁄5 Star 35⁄6 Star 35⁄7 Star 35⁄8 Star 35⁄9 Star 35⁄10 Star 35⁄11 Star 35⁄12 Star 35⁄13 Star 35⁄14 Star 35⁄15 Star 35⁄16 Star 35⁄17 36: Polygon 36 Star 36⁄2 Star 36⁄3 Star 36⁄4 Star 36⁄5 Star 36⁄6 Star 36⁄7 Star 36⁄8 Star 36⁄9 Star 36⁄10 Star 36⁄11 Star 36⁄12 Star 36⁄13 Star 36⁄14 Star 36⁄15 Star 36⁄16 Star 36⁄17 37: Polygon 37 Star 37⁄2 Star 37⁄3 Star 37⁄4 Star 37⁄5 Star 37⁄6 Star 37⁄7 Star 37⁄8 Star 37⁄9 Star 37⁄10 Star 37⁄11 Star 37⁄12 Star 37⁄13 Star 37⁄14 Star 37⁄15 Star 37⁄16 Star 37⁄17 Star 37⁄18 38: Polygon 38 Star 38⁄2 Star 38⁄3 Star 38⁄4 Star 38⁄5 Star 38⁄6 Star 38⁄7 Star 38⁄8 Star 38⁄9 Star 38⁄10 Star 38⁄11 Star 38⁄12 Star 38⁄13 Star 38⁄14 Star 38⁄15 Star 38⁄16 Star 38⁄17 Star 38⁄18 39: Polygon 39 Star 39⁄2 Star 39⁄3 Star 39⁄4 Star 39⁄5 Star 39⁄6 Star 39⁄7 Star 39⁄8 Star 39⁄9 Star 39⁄10 Star 39⁄11 Star 39⁄12 Star 39⁄13 Star 39⁄14 Star 39⁄15 Star 39⁄16 Star 39⁄17 Star 39⁄18 Star 39⁄19 40: Polygon 40 Star 40⁄2 Star 40⁄3 Star 40⁄4 Star 40⁄5 Star 40⁄6 Star 40⁄7 Star 40⁄8 Star 40⁄9 Star 40⁄10 Star 40⁄11 Star 40⁄12 Star 40⁄13 Star 40⁄14 Star 40⁄15 Star 40⁄16 Star 40⁄17 Star 40⁄18 Star 40⁄19