| Main index | Electoral System index | About author |
Julian D. A. Wiseman
Abstract: Under PR-Squared there are ‘stable’ outcomes with three parties, probably not with four, and definitely not with five or more.
Publication history: only at www.jdawiseman.com/papers/electsys/pr2_three_parties.html. Usual disclaimer and copyright terms apply.
Contents: Summary; Three parties; Four parties; Five parties; Tiny parties.
PR-Squared is a new electoral system originally designed for the UK’s House of Commons. It is described at www.jdawiseman.com/papers/electsys/pr2.html, and the PR-Squared outcome for the UK’s May 2010 election is discussed at www.jdawiseman.com/papers/electsys/pr2_uk_201005.html. It is assumed that readers are familiar with at least one of these essays.
How many serious parties there would be under PR-Squared? This essay explains that there are stable three-party outcomes, but with four parties the incentive to form pre-election coalitions becomes powerful, and for five or more parties becomes overwhelming.
The reasoning can be summarised as follows.
If there are three parties each getting approximately one third of the vote, any two can form a coalition. But if this coalition were formed after the election, the two would still have a commanding majority. Hence, for this voting pattern, there would not be an incentive to form the coalition before the election.
If there are five parties each getting approximately one fifth of the vote, then any two can form a coalition, but only if that coalition is formed before the election. Such a pre-election coalition would win (2²)/(2²+1²+1²+1²) = 4/7 ≈ 57% of the seats. With a 650-seat House of Commons this would be a very workable majority of ≈93 seats. But this happens only with a pre-election coalition: a post-election coalition would require three parties rather than two. Hence five or more parties would typically coalesce down to fewer.
If there are four parties each getting 25%±ε of the vote, things are closer. The two (slightly) smaller parties could form a majority only if they formed a coalition before the election; but the two larger parties could wait until after. However, parties wouldn’t know the exact vote count until after, so the two most similar parties would have a strong pre-election incentive to merge.
This applies even if the votes aren’t exactly equal: if they split 21% : 21% : 21% : 18.5% : 18.5% then any two could still form a majority government, if, and only if, they merged pre-election. Likewise, if votes were to split 26% : 18.5% : 18.5% : 18.5% : 18.5%, any two parties could form a coalition, but only if they did so before the election.
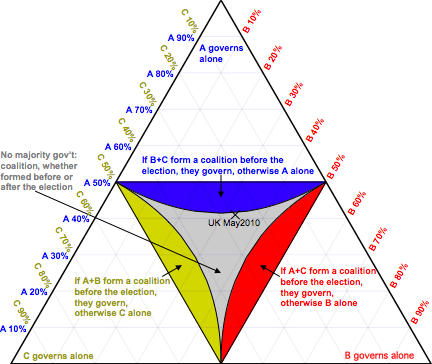
Assume that there are only three non-tiny parties. (Throughout this essay we ignore parties too small to win any seats.) Then the possibilities are shown in the chart on the right.
Any party winning over half the votes governs alone, whatever the other parties do.
If a party’s votes are between 41.42% and 50% of the total, and the two smaller parties split the remaining vote equally, then the largest party will have a majority—provided that the two smaller parties did not form a coalition before the election. In the diagram these possibilities are coloured. Of course, if the smaller parties had formed a coalition before the election, they would have had over half the votes, and would be governing. Also, if the two smaller parties split the votes non-equally, the lower bound on the size of the largest party would be larger than 41.42%.
So the area in which a pre-election coalition is incentivised is quite small: at its widest only 8.58% across, measured in terms of the votes of the largest party. Also recall that the description of PR-Squared requires that “In each constituency each party may field one candidate”, and at most one. So arranging a pre-election coalition necessitates up to half the candidates standing aside. That would take some time. But, according to the BBC, on 17th February 2009 Ipsos-Mori’s polls gave the Conservatives 48%, but on 22nd November 2009 only 37%. So at the time that such a pre-election Lib-Lab coalition would have had to be arranged, polls varied in a range of 11%, far wider than the maximum width of the region within which such a pre-election coalition would be both useful and effective.
Hence it seems likely that, under PR-Squared, there could be three non-tiny parties competing in elections. Sometimes a pair of parties would have post-election regret, in that a pre-election coalition would have kept out the other party, but such regret could not be reliably predicted.
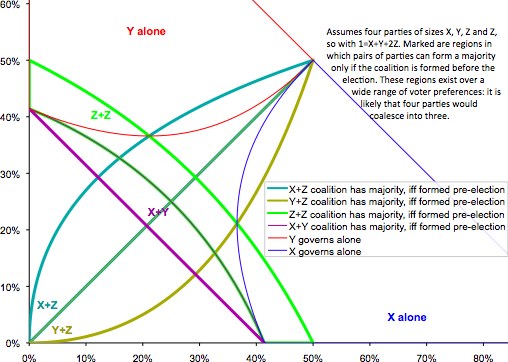
With four parties, the possible outcomes occupy three dimensions—difficult to show clearly in a browser. So, for clarity of exposition, we assume that the four parties win proportions of the vote X, Y, Z and Z, with 100% = X + Y + 2×Z. In the chart the vote of X is on the x-axis, of Y on the y-axis, and the vote of each of the Z parties is half of the remainder.
The thin blue line shows the region in which X governs alone, and likewise thin red for the region in which Y governs alone. The thick lines show regions in which a pre-election coalition would be effective (in that a pre-election coalition would have a majority of the seats), and useful (in that a post-election coalition would not have a majority). These thick lines are coloured according to the pairs of parties: X + Y; the two Z parties; X + one Z party; and Y + one Z party.
Because it is assumed that there are two parties of size Z, neither can govern alone. If X and Y are also too small to govern alone, then, over most of the remaining area of the chart, some pair or pairs of parties have an incentive to merge.
Observe that all four merger regions touch the point at which X=25% Y=25% (⇒ Z=25%). With an equal split of votes, so the more four-party-ish is the four-party system, the stronger the incentive to collapse down to three parties.
Consider the curved upper edge of the X+Z region. Everywhere to the right and below this line a pre-election X+Z coalition would have a majority (though in some of the area there would still be a majority if the coalition were post-election, and in some with X alone). That is a very large winning area: if X can tolerate the politics of either of the Zs, and X is not confident of winning alone, then a pre-election coalition would be very attractive. Equivalently, of course, for Y and the Y+Z curve.
Hence, under PR-Squared with four parties, there will be a strong incentive on various pairs of parties to merge. It is likely that, within an election or two, the number of non-tiny parties standing for election would drop to three.
(Note that the specific shape of the regions depends on the manner in which the number of dimensions was lowered by one. But the conclusion—pre-election coalitions are incentivised over large areas—is robust.)
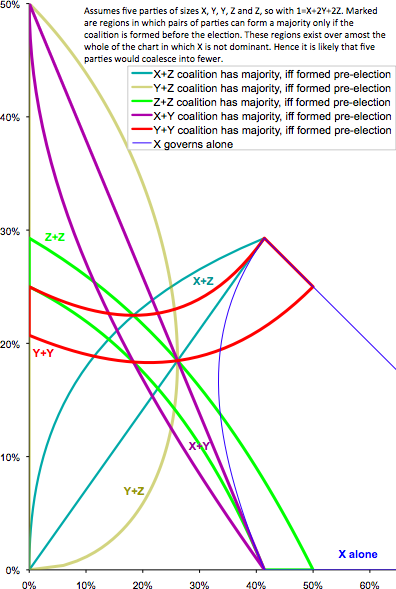
Five parties is like four parties, only more so. Again for clarity the number of dimensions is lowered, by assuming that the parties win proportions of the vote X, Y, Y, Z and Z, with 100% = X + 2×Y + 2×Z.
Because there are two parties of size Y, and two of size Z, none of these four can govern alone. But the chart on the right shows that, if X is too small to govern alone, it is very likely that some combinations of parties would have a strong incentive to merge.
Consider the point at which all five parties win 20% of the vote. A pre-election coalition would win 4/7 ≈ 57% of the seats: a substantial majority. Surely one of the ten possible pairs of parties could find enough in common to be able to agree to exclude the other three parties from their coalition government.
Hence, under PR-Squared, five non-tiny parties would be unstable, ahead of an election likely to collapse to four or three.
Note, however, that these incentives do not affect tiny parties. The UK’s Official Monster Raving Loony Party (yes, really!) does not seem to behave as a government in waiting, more as an all-purpose protest vote. Sinn Fein win a few seats in Northern Ireland, but never take them: there is not even a pretence that public policy should be determined by the outcome of elections.
Such tiny parties may well continue to exist, but, as now, are unlikely to determine who occupies 10 Downing Street.
| — Julian D. A. Wiseman Paris, 27th May 2010 www.jdawiseman.com |
| Main index | Top | About author |
There is a PR² group on Facebook. This was not created by, nor is it controlled nor endorsed by, the author, who is not a member of Facebook. Nonetheless, its existence might be of interest to some readers.