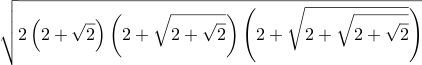
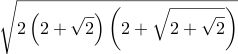
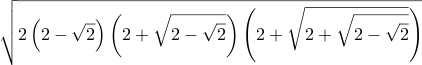
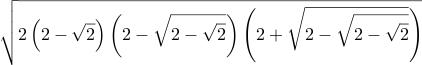
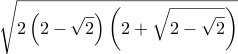
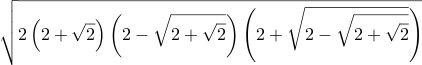
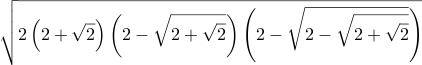
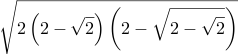
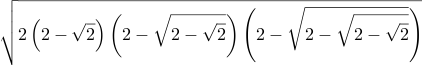
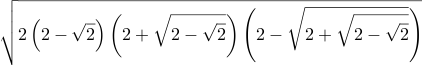
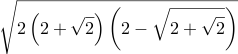
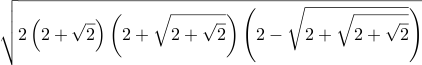
| Main index | Other Papers index | About author |
Julian D. A. Wiseman
Contents: values of Cosecant[α] = Cosec[α] = Csc[α] = 1/Sin[α] and Secant[α] = Sec[α] = 1/Cos[α], expressed in surds, for α=n×3° or α=n×5⅝°, n∈ℕ: Csc[0°], Csc[3°], Csc[5.625°], Csc[6°], Csc[9°], Csc[11.25°], Csc[12°], Csc[15°], Csc[16.875°], Csc[18°], Csc[21°], Csc[22.5°], Csc[24°], Csc[27°], Csc[28.125°], Csc[30°], Csc[33°], Csc[33.75°], Csc[36°], Csc[39°], Csc[39.375°], Csc[42°], Csc[45°], Csc[48°], Csc[50.625°], Csc[51°], Csc[54°], Csc[56.25°], Csc[57°], Csc[60°], Csc[61.875°], Csc[63°], Csc[66°], Csc[67.5°], Csc[69°], Csc[72°], Csc[73.125°], Csc[75°], Csc[78°], Csc[78.75°], Csc[81°], Csc[84°], Csc[84.375°], Csc[87°], and Csc[90°].
Publication history: only here. Usual disclaimer and copyright terms apply. Also see the values of Sin[] and Cos[], in surds, the values of Tan[] in surds, and the inner radius of n/m stars, in surds.
The table shows Cosecant[] = Cosec[] = Csc[] = 1/Sin[] and Secant[] = Sec[] = 1/Cos[] in surds, for angles that are integer multiples of 3° or of 5⅝° = 90°/16. The surds are derived from the table of values of Sin[] and Cos[] in surds, and are shown in several formats.
Graphical formula: a .png, derived from…
LaTex: a LaTeX expression.
Excel: copy-pasteable into Excel, which will automatically convert the “Sqrt” into an upper-case “SQRT”.
CalcCenter: if one enters Sqrt[2] directly into Mathematica CalcCenter (the budget version of Mathematica), it automatically evaluates the expression numerically, frustrating an attempt to work with surds. To prevent this integers inside the inner-most Sqrts have been replaced with the likes of Int5, which CalcCenter treats as a variable. If using the full-expense Mathematica instances of “Int” may be removed by a preprocessor or by setting Int2=2; Int3=3; Int5=5;.
Postscript: using 2 5 sqrt 2 mul 5 div add sqrt rather than 1 36 sin div is about as efficient computationally, but is, in some sense, far more elegant.
Help! Endeavours have been made to represent these values as simply as possible. But further simplifications would be welcomed, credit being given.
Errors: whilst the outputs have been tested, it is possible that errors remain. Please do test things before embedding them somewhere important—and if errors or possible improvements are found, tell the author.
| Csc[α] = Sec[90–α] | Graphical formula | LaTeX | Excel | CalcCenter | PostScript |
|---|---|---|---|---|---|
| Csc[0°] = Sec[90°] = ±∞ | \pm\infty | =(2^53 - 1) * (2^971) | ±Infinity | 2 23 exp 1 sub 2 104 exp mul | |
| Csc[3°] = Sec[87°] ≈ 19.107322609297 | \sqrt{4 + \left(8 + 5 \sqrt{3}\right) \left(2 + \sqrt{5}\right)} + \frac{\sqrt{2}}{2} \left(\left(2 + \sqrt{5}\right) \left(2 + \sqrt{3}\right) - 1\right) | =Sqrt(4+(8+5*Sqrt(3))*(2+Sqrt(5))) + ((2+Sqrt(5))*(2+Sqrt(3))-1)*Sqrt(2)/2 | Sqrt[4+(8+5 Sqrt[Int3]) (2+Sqrt[Int5])] + ((2+Sqrt[Int5]) (2+Sqrt[Int3])-1) Sqrt[Int2]/2 | 3 sqrt 5 sqrt 2 copy 2 add exch 2 add exch mul 1 sub 2 sqrt mul 2 div 3 1 roll 2 add exch 5 mul 8 add mul 4 add sqrt add | |
| Csc[5⅝°] = Sec[84⅜°] ≈ 10.202297237378 | 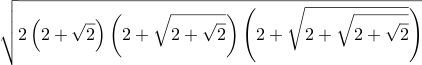 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 + \sqrt{2 + \sqrt{2}}\right) \left(2 + \sqrt{2 + \sqrt{2 + \sqrt{2}}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2+Sqrt(2+Sqrt(2))) * (2+Sqrt(2+Sqrt(2+Sqrt(2)))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2+Sqrt[2+Sqrt[Int2]]) (2+Sqrt[2+Sqrt[2+Sqrt[Int2]]]) ] | 2 sqrt 2 add dup sqrt 2 add dup sqrt 2 add mul mul 2 mul sqrt |
| Csc[6°] = Sec[84°] ≈ 9.566772233506 | \left(2 + \sqrt{5} + \sqrt{15 + 6 \sqrt{5}}\right) | =( 2 + Sqrt(5) + Sqrt(15+6*Sqrt(5)) ) | ( 2 + Sqrt[Int5] + Sqrt[15+6 Sqrt[Int5]] ) | 5 sqrt dup 6 mul 15 add sqrt add 2 add | |
| Csc[9°] = Sec[81°] ≈ 6.3924532215 | \frac{\sqrt{2}}{2} \left(3 + \sqrt{5} + \sqrt{10 + 2 \sqrt{5}}\right) | =( 3 + Sqrt(5) + Sqrt(10+2*Sqrt(5)) ) * Sqrt(2) / 2 | ( 3 + Sqrt[Int5] + Sqrt[10+2 Sqrt[Int5]] ) Sqrt[Int2] / 2 | 5 sqrt dup 2 mul 10 add sqrt add 3 add 2 sqrt mul 2 div | |
| Csc[11¼°] = Sec[78¾°] ≈ 5.125830895483 | 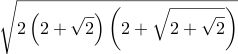 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 + \sqrt{2 + \sqrt{2}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2+Sqrt(2+Sqrt(2))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2+Sqrt[2+Sqrt[Int2]]) ] | 2 sqrt 2 add dup sqrt 2 add mul 2 mul sqrt |
| Csc[12°] = Sec[78°] ≈ 4.809734344744 | \sqrt{3} + \sqrt{5 + 2 \sqrt{5}} | =Sqrt(3) + Sqrt(5+2*Sqrt(5)) | Sqrt[Int3] + Sqrt[5+2 Sqrt[Int5]] | 5 sqrt 2 mul 5 add sqrt 3 sqrt add | |
| Csc[15°] = Sec[75°] ≈ 3.863703305156 | \sqrt{2} \left(\sqrt{3} + 1\right) | =Sqrt(2)*(Sqrt(3)+1) | Sqrt[Int2] (Sqrt[Int3]+1) | 3 sqrt 1 add 2 sqrt mul | |
| Csc[16⅞°] = Sec[73⅛°] ≈ 3.444894196477 | 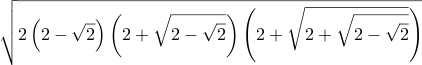 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 + \sqrt{2 - \sqrt{2}}\right) \left(2 + \sqrt{2 + \sqrt{2 - \sqrt{2}}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2+Sqrt(2-Sqrt(2))) * (2+Sqrt(2+Sqrt(2-Sqrt(2)))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2+Sqrt[2-Sqrt[Int2]]) (2+Sqrt[2+Sqrt[2-Sqrt[Int2]]]) ] | 2 2 sqrt sub dup sqrt 2 add dup sqrt 2 add mul mul 2 mul sqrt |
| Csc[18°] = Sec[72°] ≈ 3.2360679775 | \sqrt{5} + 1 | =Sqrt(5)+1 | Sqrt[Int5]+1 | 5 sqrt 1 add | |
| Csc[21°] = Sec[69°] ≈ 2.790428109625 | \sqrt{4 + \left(\sqrt{5} - 2\right) \left(5 \sqrt{3} - 8\right)} + \frac{\sqrt{2}}{2} \left(1 + \left(2 - \sqrt{3}\right) \left(\sqrt{5} - 2\right)\right) | =Sqrt(4+(Sqrt(5)-2)*(5*Sqrt(3)-8)) + (1+(2-Sqrt(3))*(Sqrt(5)-2))*Sqrt(2)/2 | Sqrt[4+(Sqrt[Int5]-2) (5 Sqrt[Int3]-8)] + (1+(2-Sqrt[Int3]) (Sqrt[Int5]-2)) Sqrt[Int2]/2 | 5 sqrt 2 sub 3 sqrt 2 copy 5 mul 8 sub mul 4 add sqrt 3 1 roll 2 sub neg mul 1 add 2 sqrt mul 2 div add | |
| Csc[22½°] = Sec[67½°] ≈ 2.613125929753 | \sqrt{4 + 2 \sqrt{2}} | =Sqrt(4+2*Sqrt(2)) | Sqrt[4+2 Sqrt[Int2]] | 2 sqrt 2 mul 4 add sqrt | |
| Csc[24°] = Sec[66°] ≈ 2.458593335574 | \sqrt{3} + \sqrt{5 - 2 \sqrt{5}} | =Sqrt(3)+Sqrt(5-2*Sqrt(5)) | Sqrt[Int3]+Sqrt[5-2 Sqrt[Int5]] | 5 sqrt -2 mul 5 add sqrt 3 sqrt add | |
| Csc[27°] = Sec[63°] ≈ 2.202689264585 | \sqrt{5 - \sqrt{5}} + \frac{\sqrt{2}}{2} \left(3 - \sqrt{5}\right) | =Sqrt(5-Sqrt(5)) + (3-Sqrt(5))*Sqrt(2)/2 | Sqrt[5-Sqrt[Int5]] + (3-Sqrt[Int5]) Sqrt[Int2]/2 | 5 sqrt dup 3 sub neg 2 sqrt mul 2 div exch 5 sub neg sqrt add | |
| Csc[28⅛°] = Sec[61⅞°] ≈ 2.121355371981 | 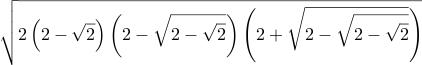 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 - \sqrt{2 - \sqrt{2}}\right) \left(2 + \sqrt{2 - \sqrt{2 - \sqrt{2}}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2-Sqrt(2-Sqrt(2))) * (2+Sqrt(2-Sqrt(2-Sqrt(2)))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2-Sqrt[2-Sqrt[Int2]]) (2+Sqrt[2-Sqrt[2-Sqrt[Int2]]]) ] | 2 2 sqrt sub dup sqrt 2 sub neg dup sqrt 2 add mul mul 2 mul sqrt |
| Csc[30°] = Sec[60°] = 2 | 2 | 2 | 2 | 2 | |
| Csc[33°] = Sec[57°] ≈ 1.836078458777 | \frac{1}{4} \left(2 \sqrt{2} \left(\left(\sqrt{3} + 2\right) \left(\sqrt{5} + 2\right) - 1\right) - \left(4 + \left(\sqrt{3} + 1\right) \left(\sqrt{5} + 1\right)\right) \sqrt{\sqrt{5} + 5}\right) | =( 2*Sqrt(2)*((Sqrt(3)+2)*(Sqrt(5)+2)-1) - (4+(Sqrt(3)+1)*(Sqrt(5)+1))*Sqrt(Sqrt(5)+5) ) / 4 | ( 2 Sqrt[Int2] ((Sqrt[Int3]+2) (Sqrt[Int5]+2)-1) - (4+(Sqrt[Int3]+1) (Sqrt[Int5]+1)) Sqrt[Sqrt[Int5]+5] ) / 4 | 5 sqrt dup 3 sqrt 2 copy 2 add exch 2 add mul 1 sub 2 sqrt mul 2 mul 4 1 roll 1 add exch 1 add mul 4 add exch 5 add sqrt mul sub 4 div | |
| Csc[33¾°] = Sec[56¼°] ≈ 1.799952446273 | 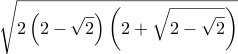 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 + \sqrt{2 - \sqrt{2}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2+Sqrt(2-Sqrt(2))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2+Sqrt[2-Sqrt[Int2]]) ] | 2 2 sqrt sub dup sqrt 2 add mul 2 mul sqrt |
| Csc[36°] = Sec[54°] ≈ 1.701301616704 | \sqrt{2 + \frac{2}{5}\sqrt{5}} | =Sqrt(2+Sqrt(5)*2/5) | Sqrt[2+Sqrt[Int5] 2/5] | 2 5 sqrt 2 mul 5 div add sqrt | |
| Csc[39°] = Sec[51°] ≈ 1.589015729066 | \frac{1}{4} \left(2 \sqrt{2} \left(\left(\sqrt{3} + 2\right) \left(\sqrt{5} - 2\right) + 1\right) + \left(4 - \left(\sqrt{3} + 1\right) \left(\sqrt{5} - 1\right)\right) \sqrt{5 - \sqrt{5}}\right) | =( 2*Sqrt(2)*((Sqrt(3)+2)*(Sqrt(5)-2)+1) + (4-(Sqrt(3)+1)*(Sqrt(5)-1))*Sqrt(5-Sqrt(5)) ) / 4 | ( 2 Sqrt[Int2] ((Sqrt[Int3]+2) (Sqrt[Int5]-2)+1) + (4-(Sqrt[Int3]+1) (Sqrt[Int5]-1)) Sqrt[5-Sqrt[Int5]] ) / 4 | 5 sqrt dup 3 sqrt 2 copy 2 add exch 2 sub mul 1 add 2 sqrt mul 2 mul 4 1 roll 1 add exch 1 sub mul 4 sub neg exch 5 sub neg sqrt mul add 4 div | |
| Csc[39⅜°] = Sec[50⅝°] ≈ 1.576309246903 | 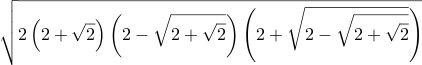 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 - \sqrt{2 + \sqrt{2}}\right) \left(2 + \sqrt{2 - \sqrt{2 + \sqrt{2}}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2-Sqrt(2+Sqrt(2))) * (2+Sqrt(2-Sqrt(2+Sqrt(2)))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2-Sqrt[2+Sqrt[Int2]]) (2+Sqrt[2-Sqrt[2+Sqrt[Int2]]]) ] | 2 sqrt 2 add dup sqrt 2 exch sub dup sqrt 2 add mul mul 2 mul sqrt |
| Csc[42°] = Sec[48°] ≈ 1.494476549865 | \sqrt{15 - 6 \sqrt{5}} + \sqrt{5} - 2 | =Sqrt(15-6*Sqrt(5)) + Sqrt(5) - 2 | Sqrt[15-6 Sqrt[Int5]] + Sqrt[Int5] - 2 | 5 sqrt dup -6 mul 15 add sqrt add 2 sub | |
| Csc[45°] = Sec[45°] ≈ 1.414213562373 | \sqrt{2} | =Sqrt(2) | Sqrt[Int2] | 2 sqrt | |
| Csc[48°] = Sec[42°] ≈ 1.345632729606 | \sqrt{5 + 2 \sqrt{5}} - \sqrt{3} | =Sqrt(5+2*Sqrt(5)) - Sqrt(3) | Sqrt[5+2 Sqrt[Int5]] - Sqrt[Int3] | 5 sqrt 2 mul 5 add sqrt 3 sqrt sub | |
| Csc[50⅝°] = Sec[39⅜°] ≈ 1.29364356672 | 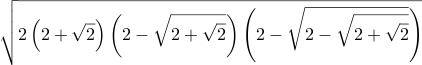 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 - \sqrt{2 + \sqrt{2}}\right) \left(2 - \sqrt{2 - \sqrt{2 + \sqrt{2}}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2-Sqrt(2+Sqrt(2))) * (2-Sqrt(2-Sqrt(2+Sqrt(2)))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2-Sqrt[2+Sqrt[Int2]]) (2-Sqrt[2-Sqrt[2+Sqrt[Int2]]]) ] | 2 sqrt 2 add dup sqrt 2 exch sub dup sqrt 2 exch sub mul mul 2 mul sqrt |
| Csc[51°] = Sec[39°] ≈ 1.286759565893 | \frac{1}{4} \left(2 \sqrt{2} \left(\left(\sqrt{3} - 2\right) \left(\sqrt{5} - 2\right) - 1\right) + \left(4 + \left(\sqrt{3} - 1\right) \left(\sqrt{5} - 1\right)\right) \sqrt{5 - \sqrt{5}}\right) | =( 2*Sqrt(2)*((Sqrt(3)-2)*(Sqrt(5)-2)-1) + (4+(Sqrt(3)-1)*(Sqrt(5)-1))*Sqrt(5-Sqrt(5)) ) / 4 | ( 2 Sqrt[Int2] ((Sqrt[Int3]-2) (Sqrt[Int5]-2)-1) + (4+(Sqrt[Int3]-1) (Sqrt[Int5]-1)) Sqrt[5-Sqrt[Int5]] ) / 4 | 5 sqrt dup 3 sqrt 2 copy 2 sub exch 2 sub mul 1 sub 2 sqrt mul 2 mul 4 1 roll 1 sub exch 1 sub mul 4 add exch 5 sub neg sqrt mul add 4 div | |
| Csc[54°] = Sec[36°] ≈ 1.2360679775 | \sqrt{5} - 1 | =Sqrt(5)-1 | Sqrt[Int5]-1 | 5 sqrt 1 sub | |
| Csc[56¼°] = Sec[33¾°] ≈ 1.20268977387 | 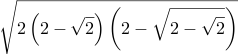 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 - \sqrt{2 - \sqrt{2}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2-Sqrt(2-Sqrt(2))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2-Sqrt[2-Sqrt[Int2]]) ] | 2 2 sqrt sub dup sqrt 2 sub neg mul 2 mul sqrt |
| Csc[57°] = Sec[33°] ≈ 1.192363292836 | \frac{1}{4} \left(2 \sqrt{2} \left(\left(2 - \sqrt{3}\right) \left(\sqrt{5} + 2\right) - 1\right) + \left(4 - \left(\sqrt{3} - 1\right) \left(\sqrt{5} + 1\right)\right) \sqrt{\sqrt{5} + 5}\right) | =( 2*Sqrt(2)*((2-Sqrt(3))*(Sqrt(5)+2)-1) + (4-(Sqrt(3)-1)*(Sqrt(5)+1))*Sqrt(Sqrt(5)+5) ) / 4 | ( 2 Sqrt[Int2] ((2-Sqrt[Int3]) (Sqrt[Int5]+2)-1) + (4-(Sqrt[Int3]-1) (Sqrt[Int5]+1)) Sqrt[Sqrt[Int5]+5] ) / 4 | 5 sqrt dup 3 sqrt 2 copy 2 sub neg exch 2 add mul 1 sub 2 sqrt mul 2 mul 4 1 roll 1 sub exch 1 add mul 4 sub neg exch 5 add sqrt mul add 4 div | |
| Csc[60°] = Sec[30°] ≈ 1.154700538379 | \frac{2}{3}\sqrt{3} | =Sqrt(3)*2/3 | Sqrt[Int3] 2/3 | 3 sqrt 2 mul 3 div | |
| Csc[61⅞°] = Sec[28⅛°] ≈ 1.133888069633 | 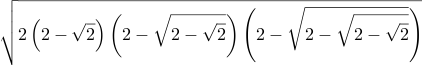 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 - \sqrt{2 - \sqrt{2}}\right) \left(2 - \sqrt{2 - \sqrt{2 - \sqrt{2}}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2-Sqrt(2-Sqrt(2))) * (2-Sqrt(2-Sqrt(2-Sqrt(2)))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2-Sqrt[2-Sqrt[Int2]]) (2-Sqrt[2-Sqrt[2-Sqrt[Int2]]]) ] | 2 2 sqrt sub dup sqrt 2 sub neg dup sqrt 2 sub neg mul mul 2 mul sqrt |
| Csc[63°] = Sec[27°] ≈ 1.122326237634 | \sqrt{5 - \sqrt{5}} - \frac{\sqrt{2}}{2} \left(3 - \sqrt{5}\right) | =Sqrt(5-Sqrt(5)) - (3-Sqrt(5))*Sqrt(2)/2 | Sqrt[5-Sqrt[Int5]] - (3-Sqrt[Int5]) Sqrt[Int2]/2 | 5 sqrt neg dup 5 add sqrt exch 3 add 2 sqrt mul 2 div sub | |
| Csc[66°] = Sec[24°] ≈ 1.094636278506 | \sqrt{15 + 6 \sqrt{5}} - \sqrt{5} - 2 | =Sqrt(15+6*Sqrt(5)) - Sqrt(5) - 2 | Sqrt[15+6 Sqrt[Int5]] - Sqrt[Int5] - 2 | 5 sqrt dup 6 mul 15 add sqrt exch sub 2 sub | |
| Csc[67½°] = Sec[22½°] ≈ 1.082392200292 | \sqrt{4 - 2 \sqrt{2}} | =Sqrt(4-2*Sqrt(2)) | Sqrt[4-2 Sqrt[Int2]] | 4 2 sqrt 2 mul sub sqrt | |
| Csc[69°] = Sec[21°] ≈ 1.071144993637 | \frac{\sqrt{2}}{2} \left(1 + \left(2 + \sqrt{3}\right) \left(\sqrt{5} - 2\right)\right) - \sqrt{4 - \left(\sqrt{5} - 2\right) \left(5 \sqrt{3} + 8\right)} | =(1+(2+Sqrt(3))*(Sqrt(5)-2))*Sqrt(2)/2 - Sqrt(4-(Sqrt(5)-2)*(5*Sqrt(3)+8)) | (1+(2+Sqrt[Int3]) (Sqrt[Int5]-2)) Sqrt[Int2]/2 - Sqrt[4-(Sqrt[Int5]-2) (5 Sqrt[Int3]+8)] | 5 sqrt 2 sub 3 sqrt 2 copy 2 add mul 1 add 2 sqrt mul 2 div 3 1 roll 5 mul 8 add mul 4 sub neg sqrt sub | |
| Csc[72°] = Sec[18°] ≈ 1.051462224238 | \sqrt{2 - \frac{2}{5}\sqrt{5}} | =Sqrt(2-Sqrt(5)*2/5) | Sqrt[2-Sqrt[Int5] 2/5] | 2 5 sqrt 2 mul 5 div sub sqrt | |
| Csc[73⅛°] = Sec[16⅞°] ≈ 1.044997229879 | 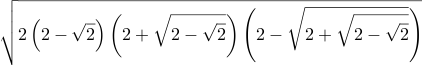 | \sqrt{2 \left(2 - \sqrt{2}\right) \left(2 + \sqrt{2 - \sqrt{2}}\right) \left(2 - \sqrt{2 + \sqrt{2 - \sqrt{2}}}\right)} | =Sqrt( 2 * (2-Sqrt(2)) * (2+Sqrt(2-Sqrt(2))) * (2-Sqrt(2+Sqrt(2-Sqrt(2)))) ) | Sqrt[ 2 (2-Sqrt[Int2]) (2+Sqrt[2-Sqrt[Int2]]) (2-Sqrt[2+Sqrt[2-Sqrt[Int2]]]) ] | 2 2 sqrt sub dup sqrt 2 add dup sqrt 2 sub neg mul mul 2 mul sqrt |
| Csc[75°] = Sec[15°] ≈ 1.03527618041 | \sqrt{2} \left(\sqrt{3} - 1\right) | =Sqrt(2)*(Sqrt(3)-1) | Sqrt[Int2] (Sqrt[Int3]-1) | 3 sqrt 1 sub 2 sqrt mul | |
| Csc[78°] = Sec[12°] ≈ 1.022340594865 | 2 - \sqrt{5} + \sqrt{15 - 6 \sqrt{5}} | =2 - Sqrt(5) + Sqrt(15-6*Sqrt(5)) | 2 - Sqrt[Int5] + Sqrt[15-6 Sqrt[Int5]] | 5 sqrt dup -6 mul 15 add sqrt sub neg 2 add | |
| Csc[78¾°] = Sec[11¼°] ≈ 1.019591158208 | 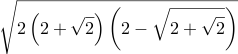 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 - \sqrt{2 + \sqrt{2}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2-Sqrt(2+Sqrt(2))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2-Sqrt[2+Sqrt[Int2]]) ] | 2 sqrt 2 add dup sqrt 2 sub neg mul 2 mul sqrt |
| Csc[81°] = Sec[9°] = 1.012465125788 | \frac{\sqrt{2}}{2} \left(3 + \sqrt{5} - \sqrt{10 + 2 \sqrt{5}}\right) | =( 3 + Sqrt(5) - Sqrt(10+2*Sqrt(5)) ) * Sqrt(2) / 2 | ( 3 + Sqrt[Int5] - Sqrt[10+2 Sqrt[Int5]] ) Sqrt[Int2] / 2 | 5 sqrt dup 2 mul 10 add sqrt sub 3 add 2 sqrt mul 2 div | |
| Csc[84°] = Sec[6°] ≈ 1.005508279564 | \sqrt{3} - \sqrt{5 - 2 \sqrt{5}} | =Sqrt(3) - Sqrt(5-2*Sqrt(5)) | Sqrt[Int3] - Sqrt[5-2 Sqrt[Int5]] | 3 sqrt 5 5 sqrt 2 mul sub sqrt sub | |
| Csc[84⅜°] = Sec[5⅝°] ≈ 1.004838572376 | 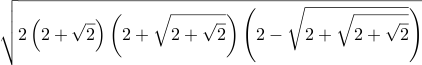 | \sqrt{2 \left(2 + \sqrt{2}\right) \left(2 + \sqrt{2 + \sqrt{2}}\right) \left(2 - \sqrt{2 + \sqrt{2 + \sqrt{2}}}\right)} | =Sqrt( 2 * (2+Sqrt(2)) * (2+Sqrt(2+Sqrt(2))) * (2-Sqrt(2+Sqrt(2+Sqrt(2)))) ) | Sqrt[ 2 (2+Sqrt[Int2]) (2+Sqrt[2+Sqrt[Int2]]) (2-Sqrt[2+Sqrt[2+Sqrt[Int2]]]) ] | 2 sqrt 2 add dup sqrt 2 add dup sqrt 2 sub neg mul mul 2 mul sqrt |
| Csc[87°] = Sec[3°] ≈ 1.001372345998 | \frac{1}{4} \left(2 \sqrt{2} \left(1 - \left(2 - \sqrt{3}\right) \left(2 + \sqrt{5}\right)\right) + \left(4 - \left(\sqrt{3} - 1\right) \left(\sqrt{5} + 1\right)\right) \sqrt{\sqrt{5} + 5}\right) | =( 2*Sqrt(2)*(1-(2-Sqrt(3))*(2+Sqrt(5))) + (4-(Sqrt(3)-1)*(Sqrt(5)+1))*Sqrt(Sqrt(5)+5) ) / 4 | ( 2 Sqrt[Int2] (1-(2-Sqrt[Int3]) (2+Sqrt[Int5])) + (4-(Sqrt[Int3]-1) (Sqrt[Int5]+1)) Sqrt[Sqrt[Int5]+5] ) / 4 | 5 sqrt dup 3 sqrt 2 copy 2 sub exch 2 add mul 1 add 2 sqrt mul 2 mul 4 1 roll 1 sub exch 1 add mul 4 sub neg exch 5 add sqrt mul add 4 div | |
| Csc[90°] = Sec[0°] = 1 | 1 | 1 | 1 | 1 |
Julian D. A. Wiseman, June 2008
| Main index | Top | About author |